Video: Pse identitetet trigonometrike janë të dobishme në zgjidhjen e ekuacioneve?
2024 Autor: Lynn Donovan | [email protected]. E modifikuara e fundit: 2023-12-15 23:53
Identitetet na mundëson të thjeshtojmë shprehjet e ndërlikuara. Ato janë mjetet bazë të trigonometria e përdorur në zgjidhjen e ekuacioneve trigonometrike , ashtu si faktorizimi, gjetja e emëruesve të përbashkët dhe përdorimi i formulave speciale janë mjetet bazë të duke zgjidhur algjebrike ekuacionet.
Atëherë, çfarë e bën një ekuacion trigonometrik një identitet?
Në matematikë, identitetet trigonometrike janë barazi që përfshijnë trigonometrike funksionet dhe janë të vërteta për çdo vlerë të variablave që ndodhin ku përcaktohen të dyja anët e barazisë. Gjeometrikisht, këto janë identitetet që përfshin funksione të caktuara të një ose më shumë këndeve.
E dini gjithashtu, cilat janë ekuacionet trigonometrike? A ekuacioni trigonometrik është ndonjë ekuacioni që përmban a trigonometrike funksionin. Siç u përmend në Trigonometrike Identitetet, a ekuacioni trigonometrik që vlen për çdo kënd quhet a trigonometrike identiteti. Ka të tjera ekuacionet , megjithatë, kjo është e vërtetë vetëm për kënde të caktuara.
Në mënyrë të ngjashme, dikush mund të pyesë, cila është mënyra më e lehtë për të zgjidhur identitetet trigonometrike?
HAPI 1: Konvertoni të gjitha sec, csc, cot dhe tan në sin dhe cos. Shumica e kësaj mund të bëhet duke përdorur koeficientin dhe reciprocitetin identitetet . HAPI 2: Kontrolloni të gjitha këndet për shuma dhe dallime dhe përdorni të përshtatshmet identitetet për t'i hequr ato. HAPI 3: Kontrolloni për shumëfisha të këndit dhe hiqni ato duke përdorur formulat e duhura.
Sa është mëkati 2x i barabartë?
sin2x =( mëkat x)2=12(1−cos( 2x )).
Recommended:
Pse janë të dobishme diagramet e rasteve?
Kur përdorni gjuhën e unifikuar të modelimit (UML), një diagram rasti i përdorimit ju ndihmon të kuptoni se si një përdorues mund të ndërveprojë me sistemin që keni projektuar. Dhe në fund, duhet të ndihmojë ekipin tuaj të përcaktojë dhe organizojë kërkesat. Në vend të kësaj, ato përfaqësojnë një përmbledhje të nivelit të lartë se si lidhen rastet e përdorimit, aktorët dhe sistemi juaj
Pse dioda Schottky është e dobishme për korrigjimin e frekuencës së lartë?
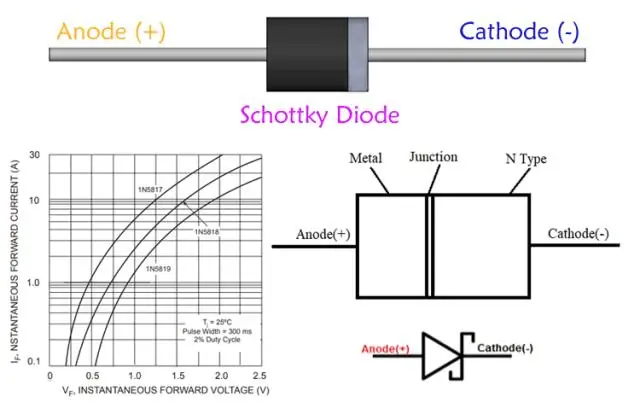
Aplikimet e diodës Schottky. Përmirësuesi i fuqisë: Diodat Schottky përdoren gjithashtu ndreqës të fuqisë ashigh. Dendësia e tyre e lartë e rrymës dhe rënia e ulët e tensionit përpara do të thotë se harxhohet më pak energji sesa u përdorën diodat e kryqëzimit PN. Schottkydiodes priren të kenë një rrymë të lartë rrjedhjeje të kundërt
Cilat janë tre burimet kryesore të të dhënave për zgjidhjen e problemeve të kërkimit të marketingut?
Tre burimet e njohurive të marketingut janë të dhënat e brendshme, të dhënat parësore dhe të dhënat dytësore. Të dhënat e brendshme janë më të përshtatshmet për monitorimin e objektivave të kostos së shitjeve, aksioneve dhe marketingut
Pse është i rëndësishëm mendimi kritik në zgjidhjen e problemeve?
Zgjidhja e problemeve dhe të menduarit kritik i referohen aftësisë për të përdorur njohuritë, faktet dhe të dhënat për të zgjidhur në mënyrë efektive problemet. Punonjësit idealë mund të mendojnë në mënyrë kritike dhe kreative, të ndajnë mendime dhe opinione, të përdorin gjykim të mirë dhe të marrin vendime
Pse janë të dobishme vlerësimet e ekspertëve?
Rishikimet e ekspertëve janë një teknikë e përdorur nga studiuesit UX për të vlerësuar përdorshmërinë e një faqe interneti ose produkti tjetër dixhital. Në fund të fundit, të dyja teknikat duhet të çojnë në një sërë rekomandimesh me përparësi për përmirësimin e përdorshmërisë dhe përvojës së përdoruesit të faqes suaj të internetit